Probability Problems( Week 47 Evaluation) 1. The probability of finding a bulb with some kind of defect in a batch of improperly produced bulbs is . Which of the following could NOT be the number of bulbs in the batch? 2. The integers 1 through 6 appear on the six faces of a cube, one on each face. If three such cubes are rolled, what is the probability that the sum of the numbers on the top faces is 17? 3. A list of integers consists of m even numbers and n odd numbers. If a number is picked at random from the list, the probability that the number is odd is . What is the value of ? 4. The probability of having head up is of the probability of having tail up in tossing an imperfect coin. What is the probability of having head up in any random toss of the coin? 5. A spinner shown in the diagram has 8 equal sections. The probability of the pointer falling into each section is the same (Assume the pointer will never fall on a line between two sections). What is the probability that the product of the two numbers that occur in two tries is an odd number?
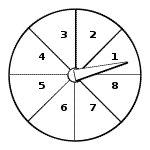
6. The product of three natural numbers is 3773. How many different sets of 3 numbers have this property (The order of the 3 numbers in a set does not matter)? 7.
The figure above shows a dartboard with 5 regions. The innermost white circle region A has a radius of 50mm and each of the circular ring regions (B, C, D, and E) has a width of 50mm also. If a dart is randomly thrown against the board, what is the probability that the dart will fall into region C? 8. A spinner shown in the diagram has 9 equal sections. The probability of the pointer falling into each section is the same (Assume the pointer will never fall on a line between two sections). What is the probability that the product of the two numbers that occur in two tries is a prime?
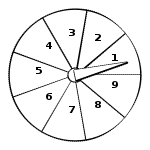
9. 20 cards are numbered 1,2,3,...,19,20, with one number per card. Martha removed 5 cards whose numbers are primes and put the remaining cards in a drawer. If one card is then picked from the drawer randomly, what is the probability that the number on the card is a prime? 10. Four people play a dice game and they are sitting around a table. If each person rolls a die (a regular die with numbers from 1 to 6), what is the probability that no one will roll the same number as the people sitting next to them? Please give your answer as a fraction in lowest terms. |