Math Olympiad 5( Week 41 Quiz 8) 1. All the customers to the restaurant ordered either hamburgers or fries or both in some day. 30 customers ordered hamburgers, 49 ordered fries, and 12 ordered both. What was the total number of customers in the day to the restaurant? 2. In the figure below, a triangle is inscribed in a circle with one of its side AC through the circle center O. If AB = 4 and BC = 12, what is the area of the circle?
3. What is the maximum area possible if a rectangle has a perimeter of 32? 4.
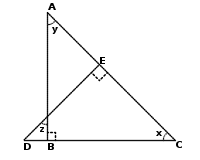
AD bisects both ∠A and the side BC of the ΔABC. Which of the following CANNOT be concluded? Note that the figure is not drawn to scale. 5. Among three friends Anne, Kevin and Nancy, only one person can drive. Anne said, "I can drive." Kevin said, "I can't drive." Nancy said, "Anne can't drive." If only one person told the truth, who can drive? 6. ABC and DEC are right triangles. If ∠D = 35° What will be x + y + z = ? Note that x, y, and z are the degrees of the corresponding marked angles, and the diagram might not be drawn to scale.
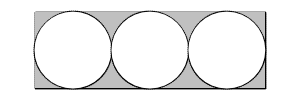
7. The measure of the smallest angle in a certain triangle is of the measures of the remaining angles. What is the measure of the smallest angle? 8. The number of the fruit candies were 6 times the number of chocolates. Emily ate 5 fruit candies and one chocolate every day. Several days later, there were 11 fruit candies left and no chocolate candies left. How many fruit candies were there originally? 9. A triangle has area of 42 square units and it can fit an incircle with a maximum diameter of 6 unit. What is the perimeter of the triangle in units? 10. Draw 6 lines across a circle, what is the greatest number of regions that the interior of the circle can be divided? 11. The circles and the enclosing rectangle are tangent as shown in the diagram. If the total area of all the circles is 45π, what is the area of the rectangle?
12. The sum of the digits in a two-digit number is 9. If the two digits exchange places, we get a new two-digit number. The new number is 63 more than the old number. What is the old number? 13. Draw 4 lines across a triangle, what is the greatest number of regions that the interior of the triangle can be divided into? 14. The sum of two whole numbers A and B is 905. The ones place value of number A is 3. If we delete the 3, then we get number B. What is number A? 15. A symmetrical number is a number that reads the same from either direction, e.g. 11, 121, 1221 are symmetrical numbers. How many 5-digit symmetrical numbers are divisible by 4? |